Strong topology (polar topology)
In functional analysis and related areas of mathematics the strong topology is the finest polar topology, the topology with the most open sets, on a dual pair. The coarsest polar topology is called weak topology.
Definition
Given a dual pair 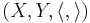 the strong topology
the strong topology 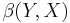 on
on  is the polar topology defined by using the family of all sets in
is the polar topology defined by using the family of all sets in  where the polar set in
where the polar set in  is absorbent.
is absorbent.
Examples
- Given a normed vector space
 and its continuous dual
and its continuous dual 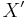 then
then 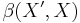 -topology on
-topology on 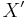 is identical to the topology induced by the operator norm. Conversely
is identical to the topology induced by the operator norm. Conversely 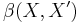 -topology on
-topology on  is identical to the topology induced by the norm.
is identical to the topology induced by the norm.
Properties
- In barrelled spaces the strong topology is identical to the Mackey topology.